Weight
Weight is one of the four forces of flight. Weight is the force of gravity on an object. For a glider, weight is equal to the combined mass of all of the components that make up the glider itself, multiplied by the acceleration due to Earth's gravity. As shown in the image below, weight opposes lift - one of the other forces of flight. Weight pulls vertically downward through the glider's center of gravity (CG). The center of gravity will be explained in more detail in the pitch stability section.
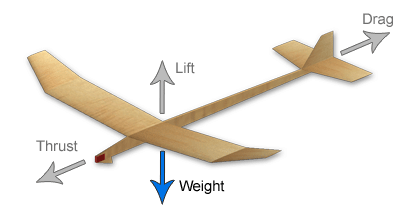
Weight Acts Through the Center of Gravity
We all have our own body weight, and can weigh ourselves on a bathroom scale. So weight should be a familiar concept. We can also determine when one object is heavier than another by picking up both objects - whichever object takes more effort to pick up, is usually the heavier object.
Gravitational force is fundamentally different from the aerodynamic forces of lift and drag. Lift and drag are mechanical forces, meaning the glider has to be in physical contact with the air to generate the force. However, a gravitational force is a field force. A field force means that two objects do not need to be in physical contact to generate a force between them. The Earth does not need to be in physical contact with the glider to generate the gravitational force.
Isaac Newton expressed the relationship between weight, mass, and gravity in a single equation:
Gravity is strongest near the surface of the Earth. The gravitational attraction between an object (let's say a glider) and the Earth weakens as the glider rises up in altitude. But near the surface of the Earth, acceleration due to gravity is relatively constant at 9.8 m/s2. This allows for the relationship in the chart below. As mass increases by 1 unit, weight will increase by 9.8 units. This is because weight is equal to mass multiplied by the acceleration due to gravity.
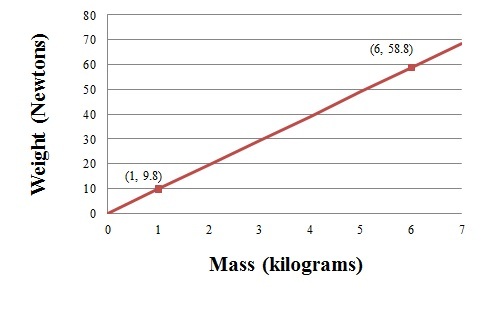
Note: A newton is the metric unit for force. One newton is the force required to accelerate a mass of one kilogram to one meter per second squared.
The weight of a glider is always directed towards the center of the Earth. The amount of weight first depends on the mass of the glider itself. Mass is a measure of the amount of matter or material an object contains. For a glider, the total mass would include the mass of the fuselage, wing, horizontal stabilizer, vertical stabilizer, and ballast. Mass and weight are directly proportional, so increasing mass will also increase weight. But as the formula for weight shows, mass and weight are not the same. Weight takes into account the gravitational pull on the mass. A glider, for example, would weigh less on the moon than it does on the Earth, even though the mass of the glider would remain the same. How is this possible? The moon is quite a bit smaller than the Earth - about 1/4 the Earth's size. This means that gravity is lower on the moon - about 1.64 m/s2.
To determine the weight of an object, we first need to know its mass. The equation for mass is:
As the formula indicates, you can alter the mass and ultimately the weight of your glider by either changing density or volume. Since density is a material property, you change density by using different materials. Using materials that have a higher density will result in higher mass (and weight). Likewise materials with a lower density will help you reduce the mass (and weight) of your glider.
| Material | Density |
|---|---|
| Balsa Wood | 0.17 g/cm3 |
| Basswood | 0.41 g/cm3 |
| Oak (Ponderosa) | 0.54 g/cm3 |
| Steel | 7.8 g/cm3 |
The equation for mass also shows us that we can change mass and weight by changing volume. The volume is the size and amount of material that you use to build the glider. If you increase volume, mass (and weight) will also increase. Mass is directly proportional to density and volume.
Action Items
The following table summarizes the independent variables that affect weight. To make the concept of weight actionable it is important to have a good understanding of which variables you can control and how you want to control them.
| Variable | Can you control this variable? | How is the variable controlled? |
|---|---|---|
| Gravity | No | Gravity is a constant (9.8 m/s2) |
| Density | Yes | Density is a material property, so you control density by the materials you choose. |
| Volume | Yes | Volume depends on the size and shape of the glider components you design and select. |
Calculating Weight
Let's calculate the mass of two different wing designs to see the impact of density and volume on mass. Using the chart from above, the density of balsa wood is about 0.17 g/cm3. Assuming the material of your wing has a size of 25 cm x 5 cm x 0.15 cm, to calculate the mass we need to first calculate the volume:
| Step 1 | Write out equation for volume | $$ \text{volume} = \text{thickness} \times \text{width} \times \text{length} $$ |
|---|---|---|
| Step 2 | Fill in the variables you know | $$ \text{volume} = 25\:\mathrm{cm} \times 5\:\mathrm{cm} \times 0.15\:\mathrm{cm} $$ |
| Step 3 | Calculate volume by combining terms (don't forget units) | $$ \text{volume} = 18.75 \:\mathrm{cm}^3 $$ |
Next we would calculate the mass:
| Step 1 | Write out equation for mass | $$ \text{mass} = \text{density} \times \text{volume} $$ |
|---|---|---|
| Step 2 | Fill in the variables you know | $$ \text{mass} = 0.17\:\mathrm{g/cm}^3 \times 18.75\:\mathrm{cm}^3 $$ |
| Step 3 | Calculate mass by combining terms (don't forget units) | $$ \text{mass} = 3.19\: \mathrm{grams} $$ |
Now that we have the mass of the wing made from balsa wood, let's calculate the mass of the same wing made from basswood. The density of basswood is 0.41 g/cm3. Like before, the wing dimensions are 25 cm x 5 cm x 0.15 cm.
Since the wing dimensions are the same as before, we can jump right to the equation for mass:
| Step 1 | Write out equation for mass | $$ \text{mass} = \text{density} \times \text{volume} $$ |
|---|---|---|
| Step 2 | Fill in the variables you know | $$ mass = 0.41\:\mathrm{g/cm}^3 \times 18.75\:\mathrm{cm}^3 $$ |
| Step 3 | Calculate mass by combining terms (don't forget units) | $$ \text{mass} = 7.69\: \mathrm{grams} $$ |
The calculations show that the mass of a balsa wood wing would be less than half the mass of a basswood wing with identical dimensions. Let's move on and calculate the weight of our balsa wood wing.
| Step 1 | We need to convert the mass in grams to kilograms | $$ \text{mass} = 3.19\:\mathrm{g} \times 0.001 = 0.00319\:\mathrm{kg} $$ |
|---|---|---|
| Step 2 | Write of the equation for weight | $$ \text{weight} = \text{mass} \times \text{gravity} $$ |
| Step 3 | Fill in the variables you know | $$ \text{weight} = 0.00319\:\mathrm{kg} \times 9.8\:\mathrm{m/s}^2 $$ |
| Step 4 | Calculate weight by combining terms (don't forget units) | $$ \text{weight} = 0.0313\:\mathrm{kgm/s}^2 \text{ or } 0.0313\:\mathrm{Newtons} $$ |