Thrust

Thrust is a force that produces lift-off, or upward movement of a rocket. Thrust acts through the center of gravity and must exceed weight in order to move the rocket off of the launch pad.

Thrust Acts Through the Center of Gravity

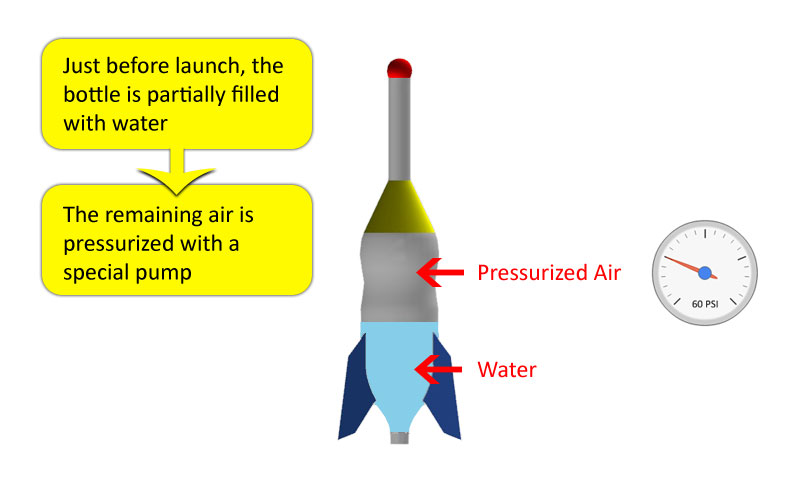
In a water rocket, a bottle is partially filled with water and a special pump is used to increase the air pressure inside the bottle. When launched, the high pressure inside the bottle forces the water out of the bottle nozzle. The ejected water leaves with a certain mass and velocity. The product of these terms is called momentum:

momentum_water = mass_water x velocity_water

Newton's Third Law of Motion will help us understand how the rocket responds to this action.

Newton's Third Law of Motion

For every action, there is an equal and opposite reaction.

This tells us that the momentum of the rocket is equal to the momentum of the water being ejected from the bottle:

momentum_water = momentum_rocket

or,

mass_water x velocity_water = mass_rocket x velocity_rocket

So how is this actionable? The relationship tells us that if we want to increase the rocket's velocity, we can do so by increasing the velocity of the ejected water, or by decreasing the mass of the rocket. How could you use this relationship to predict the rocket's performance if the bottle is simply filled with air? (Hint: the density of water is about 800 times the density of air.)

Thrust Animation

Step through the animation to see how Thrust works on a water rocket. To go to the next slide, click the blue "Next Slide" button in the lower right corner. The content of the animation is similar to the description above, but if a picture tells a thousand words a good animation will tell a lot more!

Start Animation Over

Previous Slide Next Slide

Action Items

The purpose of Thrust is to maximize rocket velocity and we can accomplish this by maximizing the velocity of the ejected water or minimizing the mass of the rocket. We learned about rocket mass in the section on weight, but how could we go about increasing the velocity of the ejected water? It is possible to determine this mathematically, but the calculations are pretty complicated. Engineers sometimes face situations in which the math is overly complicated for what they are trying to do, or in some cases the math has not yet been defined. In these situations, engineers can build physical or virtual models of a variety of designs and analyze test data to make informed design decisions.

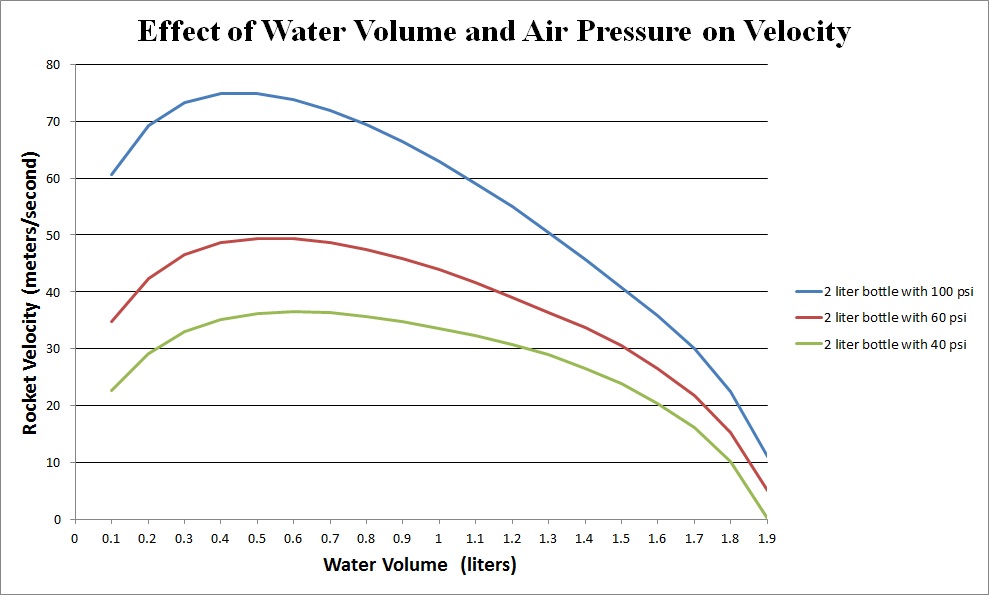
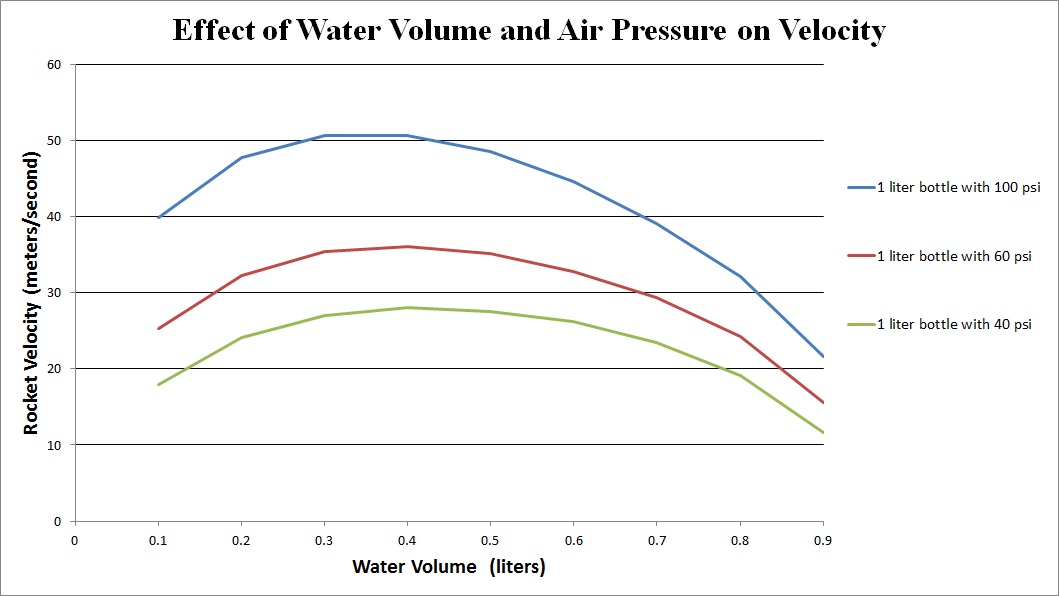
The variables that you can actually control to affect the velocity of the ejected water are bottle pressure, water volume, and bottle size. Find the graph that most accurately reflects your design constraints and use the graph to make informed decisions. Some of the questions following this section will refer to the graphs.