Drag

Drag is one of the three forces that your rocket will experience. Drag occurs when a solid object moves through a gas or liquid. When you stand in high winds, you can feel the pressure of the wind on your body. When wind speed increases, the pressure increases and this produces a force that resists forward motion. This force is drag. The force of drag acts through the Center of Pressure (CP) of the rocket. Center of Pressure will be explained in more detail in the stability section. A rocket's drag can be affected by the rocket's frontal area, shape, velocity, and air density.

To understand the force of drag you must first understand the variables involved. The equation for drag:

Drag = .5 x air density x velocity2 x frontal area x coefficient of drag
  • Air Density

    Air density changes with altitude, so the value of this variable depends on the height at which you expect to fly. For a bottle rocket, air density will remain constant due to the relatively small change in altitude. The air density for your bottle rocket is constant at 1.2 kg/m3.

  • Velocity

    Drag increases with the square of velocity. While velocity is a good thing as far as altitude is concerned, it works against us by increasing drag. Velocity is not directly controlled by you. However, changing your frontal area and drag coefficient will help change your maximum velocity.

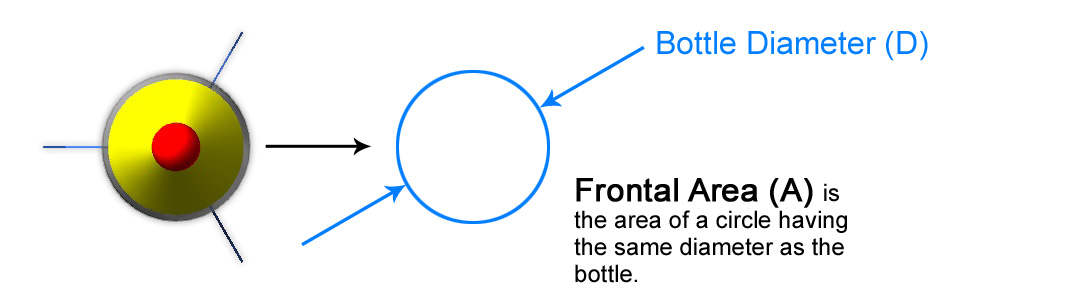
  • Frontal Area

    The frontal area is the area of the geometry you would see if the rocket were coming right at you. Increasing the frontal area will result in higher drag, so minimizing frontal area is a good way to minimize drag. The way to change your frontal area is to use a different size bottle.

    Frontal Area
  • Coefficient of Drag

    The coefficient of drag is a pretty complicated variable involving the shape of the rocket moving through the air. You can control the coefficient of drag by adjusting the shape of the transition cone. The term streamlining is used to describe adjusting the shape of an object, for example your transition cone, to reduce pressure and friction caused by air flow. Look at the three illustrations below associated with streamlining and the resulting coefficient of drag. The first (left most) design has a relatively short nose and its drag coefficient is 0.533. The second image has a longer nose and a drag coefficient of 0.364. The last design has a long nose and a drag coefficient of 0.299. Drag is directly proportional to the drag coefficient, so design decisions that result in lower drag coefficients will reduce drag.

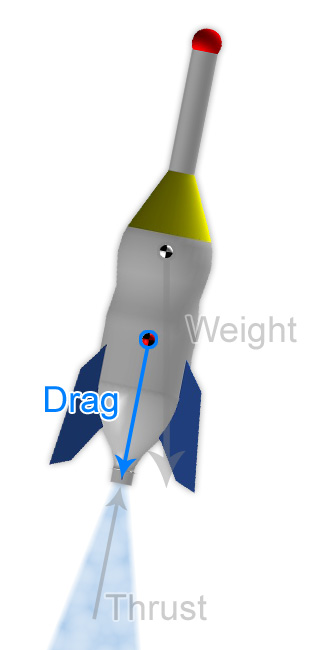
Forces on a Rocket
The Drag Force Acts Through the Center of Pressure
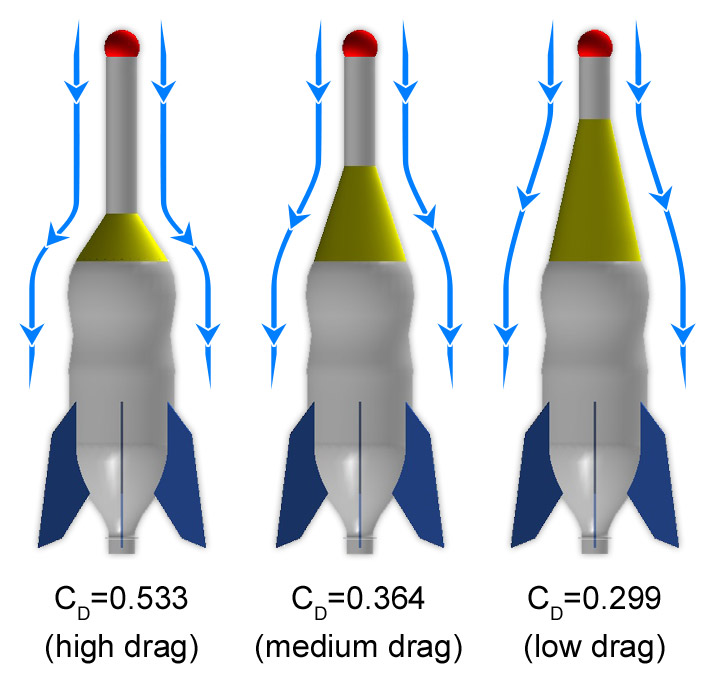
Coefficient of Drag
Examples of Coefficient of Drag

Action Items

The following table summarizes the independent variables that affect drag. To make the concept of drag actionable it is important to have a good understanding of which variables you can control and how you want to control them.

Drag Variables Can you control this variable? How is the variable controlled?
Air Density No Air density is a constant (1.2 kg/m3).
Velocity No You do not have direct control over velocity. In other words, velocity is a dependent variable. You can control velocity by changing other design variables.
Frontal Area Yes Frontal area can be changed by using a different bottle size.
Coefficient of Drag Yes The drag coefficient depends on the shape of your design - specifically the length (or interior angle) of the nose.

Now that we've established the independent variables that you can control, use the following animation to establish the relationship between these variables and drag. What happens if you increase (or decrease) the frontal area? What happens if you increase (or decrease) the drag coefficient?

Frontal Area
Drag Coefficient

Calculating Drag

Now let us work through an example problem calculating the drag on a bottle rocket.
For our example, assume we have a 2 liter bottle with:

  1. a radius of 0.0494 m
  2. a transition cone with an interior angle of 60°
  3. a velocity of 150 m/s
Step 1 Use the coefficient of drag generator to the right. Type in the interior angle of your transition cone and the generator will tell you the coefficient of drag.

Step 2 Write out equation for frontal area Frontal Area = π x radius2
Step 3 Fill in the variables you know Frontal Area = 3.141 x 0.0494 m x 0.0494 m
Step 4 Calculate area by combining terms (don't forget units) Frontal Area = 0.0077 m2
Step 5 Write out the equation for drag Drag = 0.5 x air density x velocity2 x Frontal Area x Coefficient of Drag
Step 6 Fill in the variables you know
(remember air density is constant at 1.2 kg/m3 and you determined the coefficient of drag in step 1)		 Drag = 0.5 x 1.2 kg/m3 x (150 m/s)2 x 0.0077 m2 x 0.498
Step 7 Calculate drag by combining terms (don't forget units) Drag = 51.76 kgm/s2 or 51.76 N